Magnetic fields around the most photogenic black hole
A few years ago, scientists obtained the first image of a black hole shadow. A new study presents the detection of magnetic fields at the black hole’s edge. The result takes us a step closer to understanding how the black hole launches energetic jets far into space.
ooo
Supermassive black holes are hungry monsters dwelling in the hearts of galaxies. Invisible, they patiently wait for food to stray into their domain. When an innocent star, a planet, or a cloud of gas comes too close, a black hole tears them apart with its immense gravity. The debris swirls around the black hole, creating a disk of particles. Eventually, part of the material plunges into the black hole. But some particles escape the greedy hands of the massive beast; catapulted into space, they form two incredibly fast jets.
Messier 87, or M87 for short, is a nearby galaxy harboring a black hole with a mass of about six billion times that of a Sun. That is a lot—it is one of the most massive black holes known. M87 also boasts a glorious jet1M87 was the first galaxy for which an extragalactic jet extending from its nucleus was discovered. That was in 1918, and the jet was described as a “curious straight ray.” Note that we don’t see the other jet turned away from us; the jet propagates with very high speed, beaming the emitted light away from us.
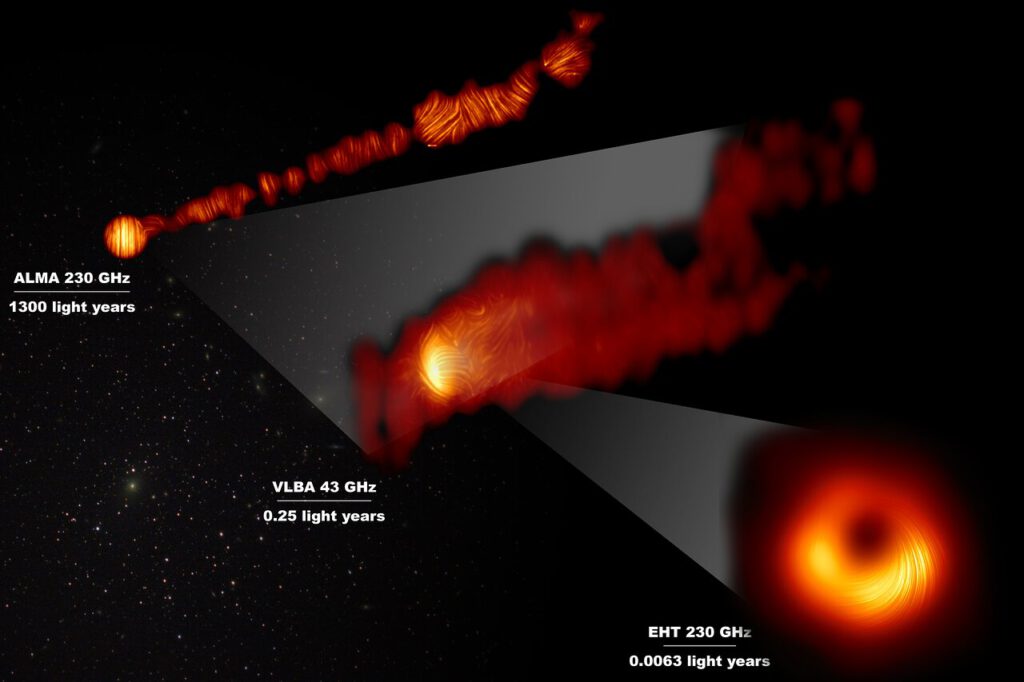
extending about 5000 light-years from the nucleus. This perfect laboratory provides an opportunity to study the conditions near the black hole. What is going on there that gives rise to a jet?

The black hole’s mass is squeezed into a region as big as our Solar system. A huge volume for a black hole2If Sun were to become a black hole—it won’t—it would have a puny diameter of about 6 kilometers., but because the galaxy is 55 million light-years away, the black hole looks tiny in the sky3About 40 microarcseconds in diameter.. How can we hope to resolve that? We would need a telescope the size of the Earth. And that is exactly what astronomers built.
The Event Horizon Telescope (EHT) is an experiment set up to observe the rim of the M87’s black hole—also called the event horizon or the point of no return beyond which the light cannot escape the black hole’s gravity—simultaneously with eight radio telescopes placed all around the world4The original black hole image and the new study about magnetic fields used observations with eight telescopes. More recently, the network expanded with three additional telescopes.. Radio light is crucial for such an experiment because it can easily pass through the dusty regions surrounding the black hole. Because the radio light has long wavelengths, one would need an enormous telescope to resolve the region around the black hole. It’s physically impossible to build a radio telescope the size of Earth, but astronomers know a neat trick to circumvent that.
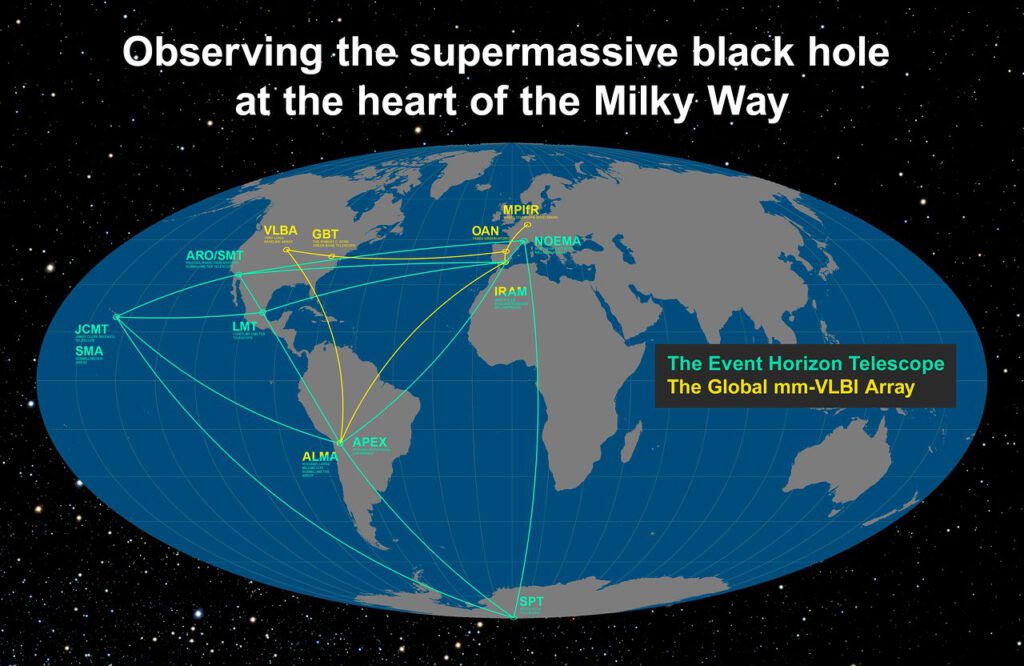
Astronomers use a technique called interferometry to achieve high angular resolutions at radio wavelengths. Radio telescopes located at different parts of the world are pointed towards a celestial object at precisely the same time. The observations are then collected and combined in a particular way. The greater the distance between the telescopes, the greater the resolution5Such simultaneous observations are demanding and require a lot of preparation and a bit of luck with the weather. Read this blog post to learn more about practical difficulties.. The EHT can achieve an incredible resolution of 20 microarcseconds6Astronomers can go pretty far (too far?) in their effort to visualize astronomical numbers. This blog describes the EHT resolution as the resolution that would allow us to stand in Chile and see through the eye of a needle in Spain. And this press release makes another helpful illustration: “The impressive resolution obtained with the EHT is equivalent to that needed to measure the length of a credit card on the surface of the Moon.”.
Observations conducted in 2017 were a big success. Scientists managed to use the data to reconstruct the first image of a black hole’s shadow. The black hole itself is invisible, but one can see the light radiated by particles rushing around it in the disk. Nevertheless, taking a photo of a black hole’s surroundings doesn’t tell you much at first glance. The immense gravity bends the path of light. Due to the warping of space-time we can see the light that was emitted behind the black hole! Light is also beamed because of the disk’s rotation with speeds close to the speed of light. Scientists had to compare observations to theoretical models to make sense of what they were seeing.
The new result goes one step further. Astronomers asked themselves: what makes a jet? Jets are still poorly understood, but most scientists agree that magnetic fields play a role. It is not easy, but there is a way to detect magnetic fields even for an object so far away as the M87 galaxy.
Light is made of electromagnetic waves that, in principle, can oscillate in every direction. But in the presence of magnetic fields, particles can emit light that oscillates in a preferred direction. We say that the light is polarized. The level and orientation of polarization teach us about magnetic fields. Some of the EHT’s radio observations not only collected radio light but also measured its polarization. After tedious calibration efforts, scientists created the first polarization map close to a supermassive black hole.
Scientists found a varying polarization in the ring around the black hole. The strong gravity and high speeds once again scramble the information. Scientists simulated a suite of possible physical scenarios, using complicated numerical codes that take into account light emission and propagation in the presence of magnetic fields. Comparing the results to the observed polarization patterns, they could narrow down the probable conditions in the disk.
The observed strength and pattern of polarization point toward a so-called magnetically arrested disk. This technical term describes a situation in which the magnetic field is strong enough to stop the material from flowing onto the black hole. “The observations suggest that the magnetic fields at the black hole’s edge are strong enough to push back on the hot gas and help it resist gravity’s pull. Only the gas that slips through the field can spiral inwards to the event horizon,” explains Jason Dexter, Assistant Professor at the University of Colorado Boulder, US, and Coordinator of the EHT Theory Working Group.
Models suggest that the polarization should change with time and frequency. The EHT project will continue, and new observations will be able to test the predictions and therefore put better constraints on the models. On the other hand, the interplay between black holes, disks, and jets is very complicated, and theoreticians will have to improve their models to get the most out of the incredible data set.
Studies like this illustrate the interdependency between observations and theory. One cannot go without the other.
Further reading:
ESO press release
Observational paper
Theoretical paper